이 장에서는 앞서 다루지 않았던 암호화 유형에 대해 다룰 것이다.
Public Key Encryption
Digital Signature에 대해 다룰 것이다.
Public Key Encryption := 비대칭키 알고리즘
사용자의 공개키와, 비공개키가 쌍을 이루어 암호화, 복호화를 진행한다. 보내고 싶은 메시지를 수신자의 공개키로 암호화하면 수신자는 자신의 비공개키로 이를 복호화하여 메시지를 확인한다.
공개키는 공개되어 있어 누구나 특정 수신자에게 메시지를 보낼 수 있지만
비공개키는 수신자 자신만 알고 있기 때문에 암호화된 메시지는 수신자 자신만 읽을 수 있다.
Crypto based on factoring : 인수분해를 활용한 암호화
엄청 큰 하나의 합성수를 두 소수로 인수분해하는 것이 어렵다는 점에서 착안한 암호화 방식이다.
또한 그 소수를 찾더라도 그 수가 key인지 맞추는게 어려운 알고리즘
RSA : 인수분해 기반 대표 알고리즘
(2020년엔 250자리수까지 인수분해가 되었고, 2019년엔 240자리까지 인수분해 되었다.)
숫자가 클수록 인수분해가 어렵다는 특징을 활용한다.
1. 큰 두 소수 p,q를 정한다.
2. N = pq라 하고 이는 나누는 수 (modulus)로 활용한다.
3. (p-1)*(q-1)과 서로소인 e를 정한다. (여기가 Randomness 포인트 1)
4. ed = 1 {mod (p-1)*(q-1)}인 d를 정한다. (여기가 Randomness 포인트 2)
Public key : (N,e)
Private key : d
이렇게 비대칭키쌍을 정했다.
보낼 메시지 평문 M을 정한다. (단, M<N)
암호화 : C = M^e (mod N)
복호화 : M = C^d (mod N)
따라서, N = pq로 인수분해가 되어 p,q가 구해지면 적절한 e,d를 찾아 암호화가 뚫릴 수도 있다!
암/복호화 과정은 오일러의 정리 / 페르마의 소정리를 통해 증명할 수 있다.
파이(N) = (p-1)(q-1) // p*q와 서로소인 원소의 개수
실제 숫자 예시 |
p=11 , q=3 (p,q 비공개)
N = p*q = 33 (N은 public key)
(p-1)*(q-1)과 서로소인 e를 구하라. e =3
ed = 1 mod (p-1)(q-1) d = 7
따라서, 공개키는 (N,e) 비공개 개인키는 d = 7
주의 사항
세 제곱근 공격
e가 너무 작아서 (e=3) 평문 M^e mod N을 해도 실제 mod 연산을 거치치 않아 원래의 값 유추가 쉬워지는 공격.
M이 N^(1/3)보다 작으면 중국인의 나머지 정리를 활용해 암호화가 뚫릴 수 있다.
중국인의 나머지 정리?
여러 합동식이 하나의 해를 가르키는 경우에 하나의 해를 추측할 수 있다.
x = a1 mod n1
x = a2 mod n2 .... 이런식이 많음녀 x를 쉽게 구할 수 있다.
가령 e = 3인 여러 대상에게 M을 암호화해서 보낸다하자. 이때, M^3 = c1 mod n1, M^3 = c2 mod n2, M^3 = c3 mod n3이므로, M^3 mod N = C인 C를 구할 수 있다.
이때 M^3 < N이면 mod 연산을 거치지 않고 C를 알게 되고 C를 적당히 세제곱근을 구하면 개인키 d가 없이도 평문으로 복호화를 할 수 있다.
모듈로 연산 쉽게하는 방법
쪼개서 분할 연산 가능함!
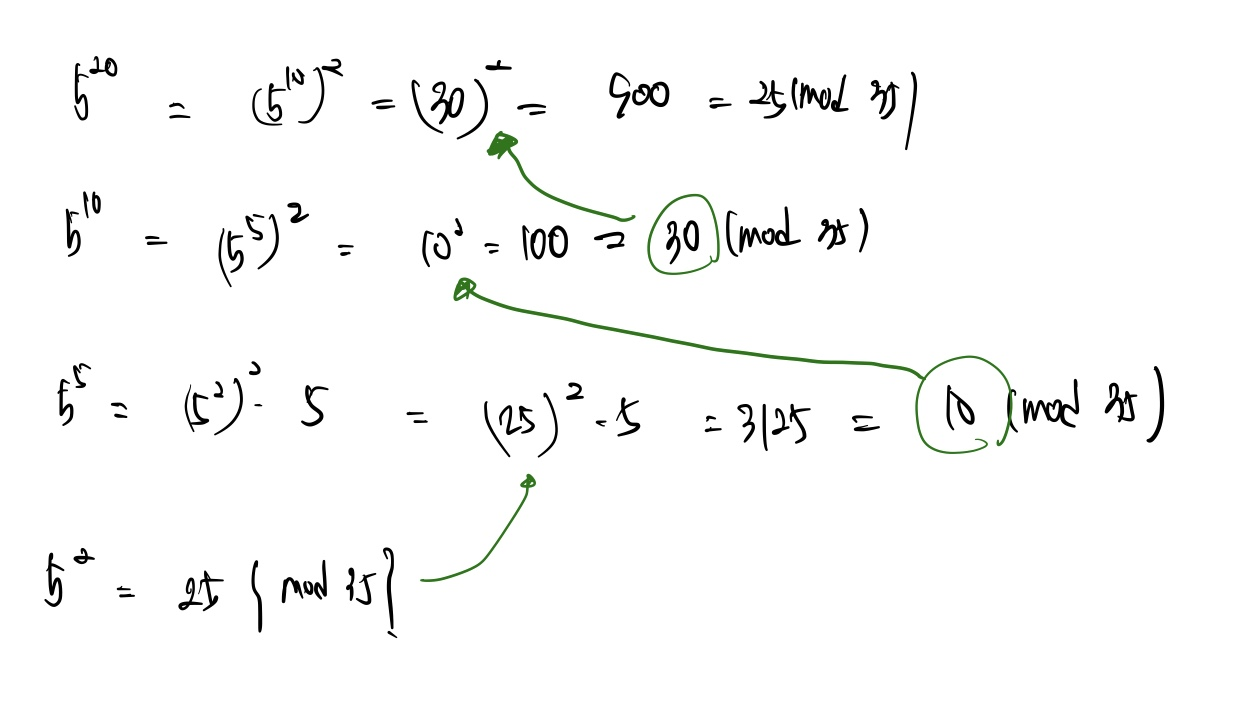
Crypto based on discrete logarithms : 이산 로그를 활용한 암호화
Diffie-Hellman KE : 공유 대칭키
각자의 개인키를 이용해 값을 보내고 교환 받은 값을 기반으로 공유대칭키를 만드는 암호학
p,g가 공개되어있고 Alice의 개인키가 x, Bob의 개인키가 y라고 하자.
이때 아래와 같이 상호교환이 일어난다.

이 교환 이후, Alice는 x와 g^y를 가지고 있고 Bob은 y와 g^x를 가지고 있어 이를 활용해 아래식으로 공유대칭키를 만든다.
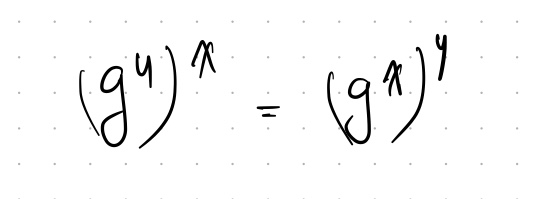
이제 A와 B는 이를 key로 활용해 암호를 주고 받을 것이며, 이 키는 제곱에 mod에.. 웬만해서 뚫리기는 어렵다.
하지만!! 이 Diffie-hellman 역시 취약점이 있는데..
Meet in the middle Attack : MIM attack
Alice와 bob이 통신할때 가운데에 제3자 Trudy가 껴서 자신과의 키를 만드는 것

위의 그림처럼 Alice, Bob 사이에 Trudy가 있다. Trudy가 사이에서 Alice와 Bob에게 서로의 값인 양 자신의 값을 전달하면 Alice와의 키 k1을 만들고 Bob과의 키 K2를 만들 수 있다.
완전한 암호는 아니다!
ElGamal digital signature : 서명 얘기
서명에 대해 먼저 이야기해보자.
내가 암호화를 아무리 잘해서 보내도 MIM과 같이 중간에서 누가 메시지 자체를 훼손하고 수정해버리면 답이 없지 않는가? 따라서, 이 메시지가 진짜 내가 커뮤니케이션하려는 상대임을 증명할 서명 방법이 필요하다.
ElGmal 서명은 디피헬만의 확정 버전으로 서명에 관한 이야기를 한다.
Alice가 개인키 X로 서명을 한다.
공개된 서명값 Y = g^x mod p이다.
이제 Alice가 메시지 M을 보낸다고 가정하자.
p,g 공개됨
m : M을 해시로 축약한것.
k : Random key(비공개)
r = g^k mod p
s = k + mX mod (p-1)을 계산한다.
Alice는 상대에게 M (r,s)를 보낸다.
이제 이 메시지를 받은 상대는 어떻게 이를 검증할까?
전달받는것 M, (r,s)
알고 있는 것 Y (= g^x mod p)
M을 기반으로 해시해서 m을 얻고
g^s = r * Y^m mod p와 같은 값을 같는지 확인한다.
해당 내용이 증명되면 Alice가 보낸 내용이 맞다는게 증명된것이다!
Y 역시 Alice만 만들 수 있는 고유의 값이고 r,s역시 k를 아는 Alice가 아는 고유의 값인데 이 두개가 같다는 이야기니말이다!
이를 통해 메시지를 보낼때 메시지가 중간에 변조되지 않았음을 확인하기 위해 M, h(M)을 일반적으로 같이 보내는데 이 둘이 동시에 수정될 가능성이 사라졌다.
수신자는 Y를 이미 알고 있으니, M과 주어진 값으로 구한 Y가 다르면 아! 내가 원하는 송신자가 보낸게 아니구나를 확인할 수 있다.
Elliptic curve cryptography : ECC 타원곡선 기반 암호화
이는 앞서 다룬 인수분해, 이산로그가 아닌 타원 곡선 그래프로 공개키, 개인키를 정하는 암호방식이다.
RSA를 사용할때에는 인수분해를 어렵게 하기 위해 Key의 길이가 계속 늘어나고 계산이 느려진다는 단점이 존재했다.
그러나, 효율적이다.
- ECC는 같은 수준의 보안성을 Shorter key로 제공해준다.
- 성능 도한 서명, 서명+검증이 매우 빠르다.
- key를 저장할 공간이 적게 든다
- 낮은 대역폭이든다.
RSA는 기존 표본 set으로 새로운 값이 나오면 유추가 가능하지다. 그러나 ECC는 타원곡선을 기반으로해 값이 다양하고 양자내성이 있다!
(물론 이론상 유한시간내에 풀리지만..)
타원곡선의 기본형은 다음과 같다.
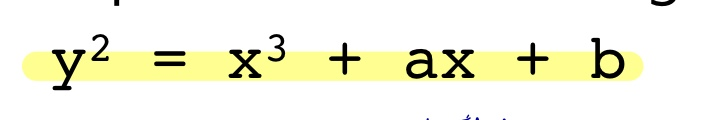
이를 ECC에서는 mod p를 사용해 가능한 결과의 범위를(0~p-1) 유한체 집합으로 만든다 (Galois field)
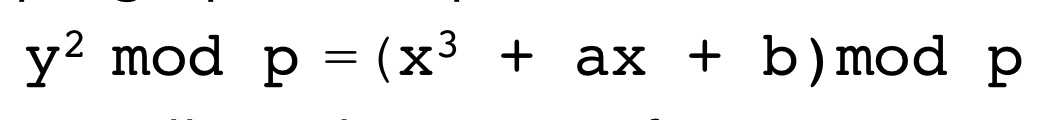
새로운 개념의 덧셈
타원 곡선에서 정의하는 덧셈의 개념은 일반적으로 다르다.
P1 (1,4) , P2(3,1)이라고 생각하면 일반적으로 P1 + P2 = P3일때, P3 = (4,5)라고 생각하겠지만 여기선 새로운 개념의 덧셈이 들어간다.
- 직선 P1P2를 그린다.
- 이 직선과 타원곡선내의 다른 교점을 찾는다.
- 이 교점을 X축 대칭해서 얻게되는 점P3를 덧셈의 결과로 한다.
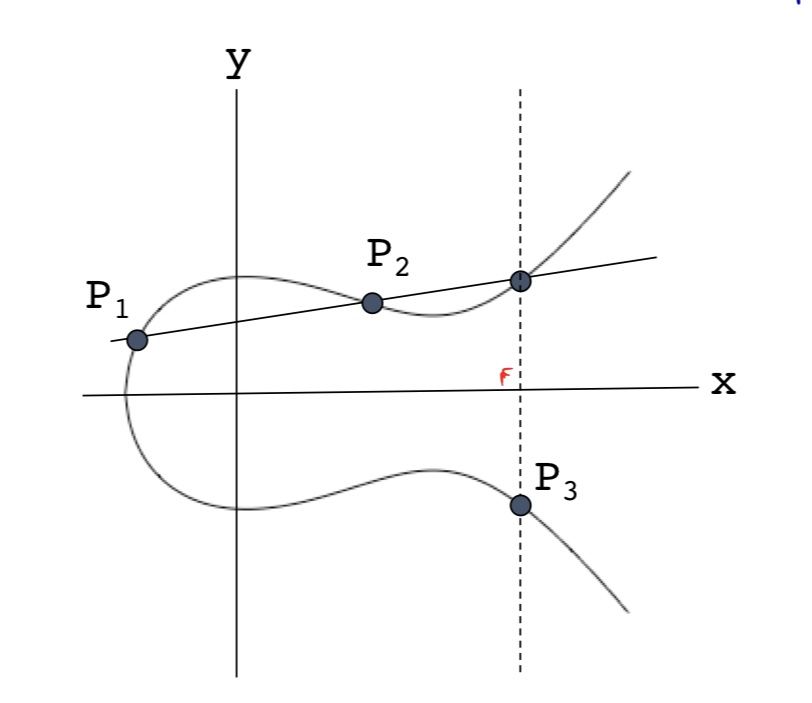
식으로 P3를 구하는 공식
우선 m을 알아야한다. m을 구하는 과정은 p1 == p2여부에 따라 다르다.
x3 = m과 x좌표들로
y3 = m과 x3, p1을 활용해 구한다.

어떻게 활용함?
base point G를 x번 더해서 a를 얻는다고 하자.
a = xG로 a를 구한다.
이때, 공개된 a,G --> x는 어렵지만
x,G --> a는 쉽다!
공개키 : a,G
비공개키 : x
ECC Diffie-Hellman
ECC를 통해 공유 대칭키를 만드는 과정
dA = 4
dB = 7
이고 알려진 base point = (2,5)
Alice --> Bob 4(2,5) = (7,32)
Bob --> Alice 7(2,5) = (18,35)
이를 받은 각자는 다음과 같은 계산을 한다.
Alice : 4(18,35) = (22,1)
Bob : 7(7,32) = (22,1)
각자 서로의 개인키는 모르지만, 자신의 개인키로 값을 공유하고, 개인키로 공유키를 계산했더니 공유대칭키 (22,1)이 등장했다.
실제 (22,1)은 base point를 4*7 = 28번 곱한 값이지만, 서로는 여전히 서로의 개인키를 모른다.
ECC 서명 / 검증
서명
송신자 : 보낼 메시지 m, 계산된값 (r,s)전달
개인 (dA, k)
검증
수신자 : m --> z = h(m) 구하고, r,s,z활용해서 u1, u2 구함
(x1,y1) = u1G + u2Qa를 구하는데 (Qa가 Alice가 보냄을 증명하는 공개된 값)
r == x1인지 확인하여 검증
즉, 여기도 서명과 보낸 값이 맞는지를 비교해 송신자를 체크한다.
Pulice key Crypto의 성질
- Confidentiality
- Authentication
- Digital signature 을 통한 Intergrity and Non - Repudiattion
기밀성과 인증은 대칭키에서도 보장하는 성질이지만
Non - Repudiation은 아니다!
Non - Repudiation : 부인 봉쇄성
내가 한 것을 안했다고 할 수 없다
대칭키에서 생각해보자.
Alice가 Bob 대칭키로 주식을 주문한다. 이때 MAC을 활용해서 주문 내역이 변함이 없다는 것 즉, 무결성을 확보한다.
Alice는 주식이 떨어지자 주문 자체를 취소하고 싶어진다.
Alice한테 너가 주문했잖아!!!!! 라고 할 수 있을까?
아니다, MAC을 만들기 위해 사용된 키는 bob하고도 공유하는 대칭키이기에 Bob이 주문한 것이라는 주장을 할 수 있다.
이제 비대칭키, 공개키 암호화로 생각해보면
Alice가 자신의 개인키로 서명을 하고 이가 Alice의 공개키로 검증이 되면 해당 주문을 부인할 수 있을까?
아니다. 우리는 자신이 아니라고 부인할 수 없는 것을 막는 이 성질을 부인 봉쇄성이라고 한다.
선 서명 후 암호화
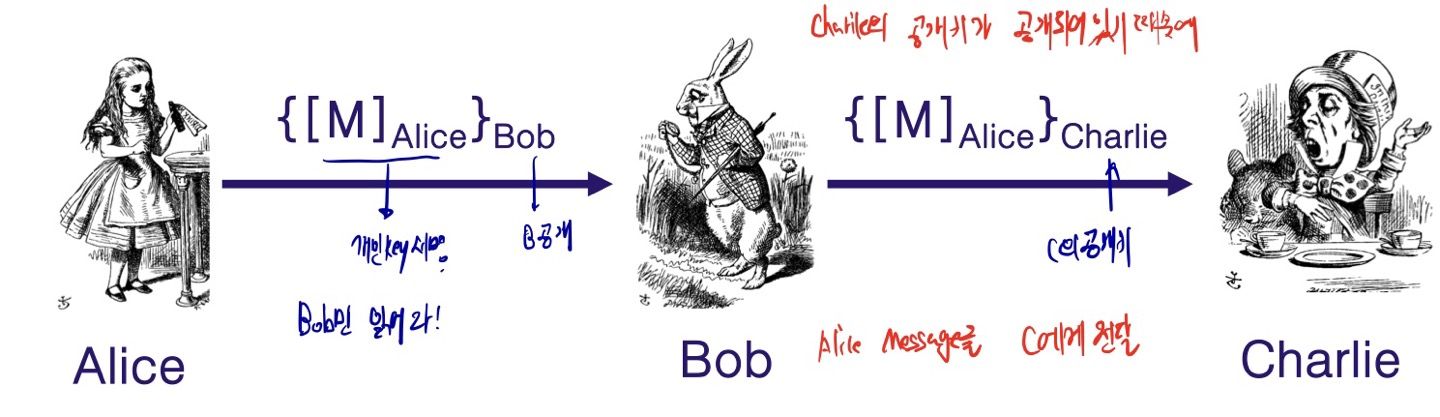
Alice의 서명을 get한 수신자가 타인에게 메시지를 전달할 수 있다.
수신자가 나쁜마음 가능
선 암호화 후 서명
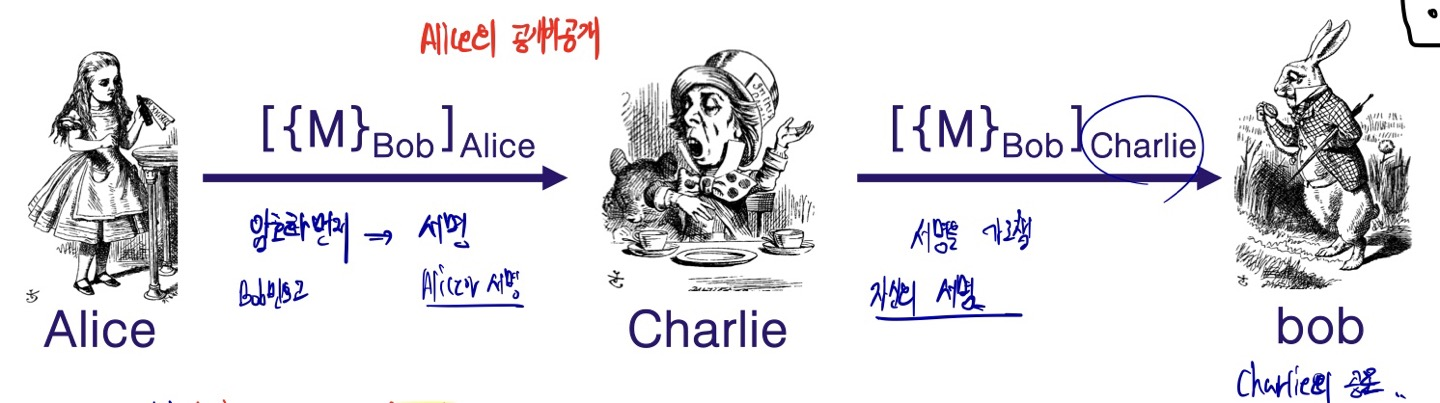
중간에 제3자가 가로채 메시지를 자신이 보낸듯 할 수 있다.
송신자를 바꿀 수 있다.
PKI : Public - key Infrastructure
공개키가 진짜 그 사람 공개키가 맞는지 보증하는 기관
PKI Trust Model
Monopoly model : 완전 독점
CA를 하나만 만들자! 여러개는 자원 낭비야
이때 중앙화된 CA에 문제가 생기면...
Oligarchy : 소수 독점
여러개의 소수의 CA를 만들고 등록하자
현재 Browser에서 쓰이는 방법.
Anarchy model : 완전 자유
개개인이 모두 CA이다!
Q&A
- 중국인의 나머지 정리 세제곱근 공격 설명할때 m^3 = C1 mod n1, ,, m^3 = C mod (n1*n2*n3)라고 했는데 별 작업 없이 세제곱근 평문을 구할 수 있는게 문제인것?
중국인의 나머지 정리에 의해 여러개의 모듈러식이 하나의 해를 가르키면 해당 해인 m^3을 찾을 수 있다.
얻어진 C = M^3 mod N이고 M^3<N이기에 C = M^3 C의 세제곱근을 구하면 평문을 찾을 수 있다.
즉, 개인키 d가 없이도 복호화가 가능하다.
- 1/2 mod 5 가 3인 이유
- a = x*G라고 했는데 G인 base point는 한 점을 두 번 더하는 것인지?
타원곡선에서의 덧셈은 P1P2를 지나는 직선과 타원 곡선이 만나는 점을 찾고 , x축 대칭하는 것, 그러면 같은점을 지나는 직선..? 이건,, 그냥 식 기준으로 이해할까요?
Yes, 식으로 생각하라
- 서명 M, hash값 둘 다 수정되면? y가 있잖아 Elgamel
'CS > 정보보안' 카테고리의 다른 글
| 정보보안_6_Protocol (0) | 2023.04.22 |
|---|---|
| 정보보안_5_Authentication (1) | 2023.04.20 |
| 정보보안_3_Crypto (0) | 2023.04.13 |
| 정보보안_2_Crypto (1) | 2023.04.12 |
| 정보보안_1_introduction (0) | 2023.04.11 |
