Crypto는 아래 3가지의 개념을 포괄하는 개념이다.
1) Cryptography : the science and arr of desiging ciphers. 암호코드를 만드는것
2) Cryptanalysis : breaking secret codes. 암호를 해독하는 것
3) Cryptology : 암호학문 그자체
Encrypt : 평문 --> 암호문
Decrypt : 암호문 --> 평문
이 사이를 암호화하고 해독하려면 key가 필요함!
기본적인 가정
System, 알고리즘은 알려져있다.
오직 key만 secret. 즉, Key가 노출되면 안된다.
이 가정을 하는 이유?
암호 알고리즘이 노출되었을때 더 취약함
알고리즘은 결국 노출된다.
오히려 미리 약점을 찾아내는것이 낫다.
Historic
Shift Cipher : 이동 암호 K만큼 알파벳 이동하기
Transposition Cipher : 암호문의 순서를 뒤바꾸는것 (재배치)
Substitution Cipher : 치환 암호 --> 빈도분석으로 찾을 수 있다는 단점.
Perfect secrecy
아래의 두 가지가 충족되어야함.
1. Computational security : 가장 효율적인 알고리즘 계산 방법으로 계산을 해도 암호를 풀려면 현재 하드웨어의 최대계산 이상의 계산이 필요하다.
2. Unconditional security : 상대가 무한한 계산이 가능하더라도 평문과 암호문의 연관성을 찾을 수 없음.
따라서, Brute Force로 전수계산을 하는게 가장 효율적인 해독방법이면 해당 Cryptosystem은 secure하다.
반대로, Shorcut이 존재하면 Cryptosystem은 Insecure하다.
Historical CIpher
Vigenere cipher
Key로 문자열을 정해서 해당 문자열만큼 더한다.
EX
Plain : YOUN
KEY : CAN
CIPHER : YOUN + CANC = ... (Key는 길이가 다르더라도 반복된다.)
Vernam Cipher / One-time Pad
Key와 원문의 길이는 항상 동일함
단, 키는 무작위하고 랜덤으로 생성되며 일회성, 한번만 사용하고 버린다.
키와 원문을 XOR연산을 통해 암호화 한다.
해당 키로 다시 XOR연산을 하면 복호화가 가능하다.
즉, 키는 미리 사전에 공유되어있어야한다.
원문 XOR KEY = 암호문
암호문 XOR KEY = 원문
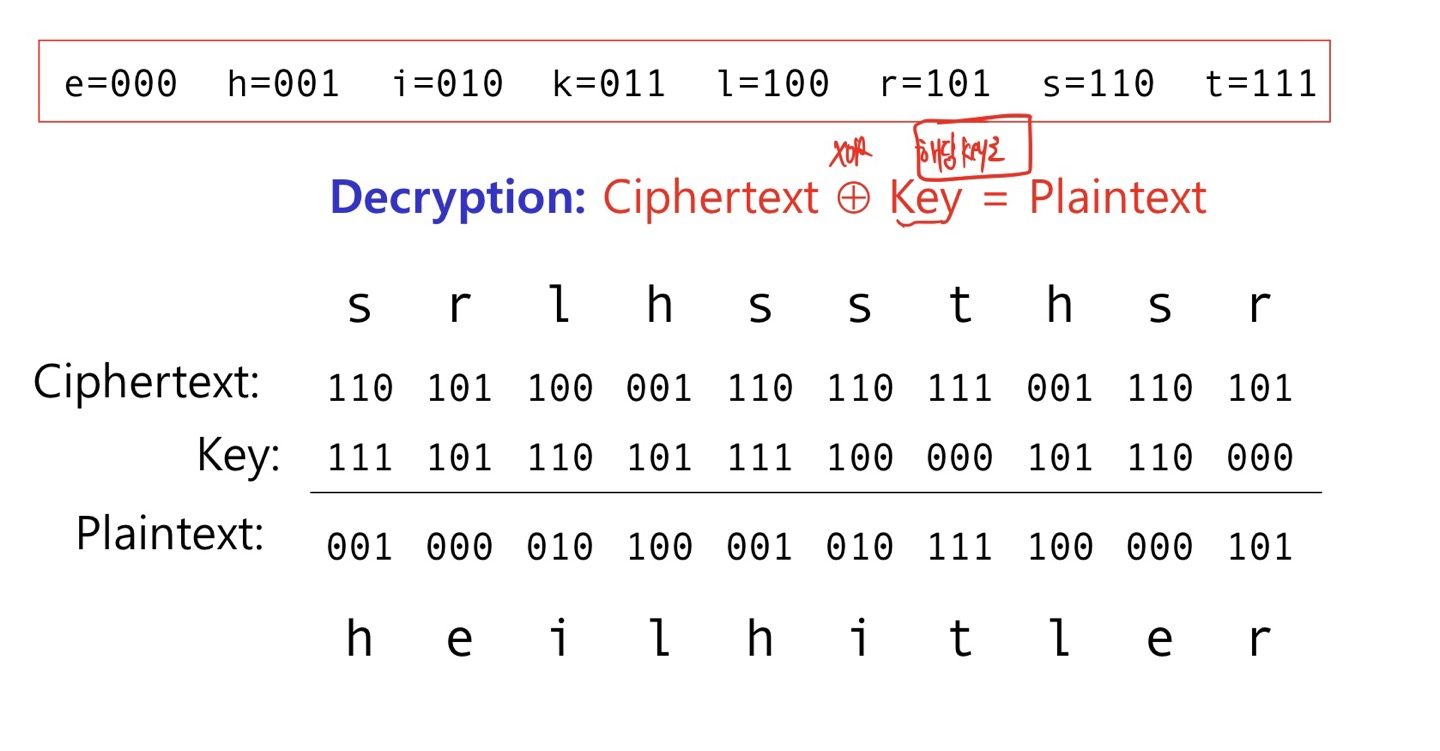
One time pad는 동일한 key를 두 번 사용하지 않는다는 전제하에 Perfect Secrey를 만족한다.
길이정보외에는 평문과의 어떠한 관계를 찾을 수 없다.
단, 키를 두 번 이상 사용하게 되면 유추가 가능해진다.
완벽한 방법이지만, key의 길이가 길어 메시지 수의 제한이 있다는 점등에서 현실적으로 실현하기 어렵다는 단점이 있다.
CodeBook Cipher : Code와 단어를 매칭한 book
Ex : Zimmerman Telegram
현재 Block CIpher의 한 예시이다.
Types of Cipher
- Random Function -> Hash Function
- Random Generators -> Stream ciphers
- Random permutations -> block ciphers
- public key encryption
- Digital Signatures
등이 존재한다.
1. Hash Function
해쉬 함수는 사실 키를 사용하지 않고 그저 함수 자체이다. 해시함수를 통한 암호화는 5가지의 성질을 띈다.
1) Compression : 결과값의 Bit수가 고정되어있기에 output length 가 줄어들어 압축성을 띈다.
2) Efficiency : H(x) 계산만 하면 되기에 연산이 간단하다. 따라서, 효율적이다.
3) One-Way : 입력값 x -> y는 찾기 쉽다. 그러나 반대로 결과값 y를 보고 x를 유추하기는 어렵다. 단방향성을 띈다.
(해당 성질을 이용해 a메시지의 무결성을 확인할 수 있다.)
4) Weak collision resisteance : 약한 충돌 저항성, 주어진 x, h(x)에 대하여 x!=y인데 h(x) == h(y)인 y를 찾기 어렵다.
5) Strong collision resisteance : 강한 충돌 저항성, 아무것도 주어지지 않았을때, x!=y 이며 h(x) == h(y)인 x,y 쌍을 찾기 어렵다.
여기가 조금 헷갈리는데 weak니까 조건이 주어져야하고 하나만 찾으면 되고 Strong이니까 아무것도 안주어져도 2쌍을 찾아야한다는 걸로 생각하자!
Pre-Birthday Problem
N명이 같이 모여있다고 할때, 나와 생일이 같은 사람이 존재할 확률을 알고 싶다. 존재할 확률이 0.5 이상이라면 내기에서 존재한다에 거는것이 유리하다. 이를 해결해보자.

N이 253명 이상일때 나와 같은 생일자가 존재할 확률이 절반을 넘어간다. 즉, 나와 생일 같은 사람이 존재하려면 많은 사람이 필요하다는걸 알 수 있는데...
Birthday Paradox
그렇다면 생각해보자. N명의 사람이 모여있을때 임의의 2명의 생일이 동일할 확률은 얼마일까? 해당 확률이 0.5가 넘어간다면 내기를 할때 넘어간다에 거는 것이 유리하다.
과연 앞에서 Pre-birthday에서 보았던 것처럼 N이 커야지만 확률이 높을까?
아니다. 실제로 N = 23만 되어도 23명중에 생일이 같은 두명이 존재할 확률이 50퍼센트를 넘는다.
N이 23이상이라면 존재한다에 거는게 유리하다는 것이다.
증명은 아무튼 뒤로하고.
여기서 알 수 있는 것은 특정값과 같은 해시값을 찾는 것은 쉽지 않다. (Pre-Birthday problem)
그러나, 해시값이 동일한 임의의 서로 다른 두 숫자를 찾는 것은 쉬울법하다는 이야기이다. (Birthday Paradox)
실제로 N bit의 결과를 내는 해시함수의 충돌을 찾으려면 2^(n-1)의 연산을 해야한다고 생각하지만 사실은 2^(n/2)정도의 연산만으로도 충분하다는 것이다.
N = 10이면 1024번 가까운 연산을 해야 충돌을 찾는 것이 아니라, 2^5 = 32번의 연산이면 평균적으로 충돌을 찾을만 하다는 것이다.
Popular Cryptographic Hashes
1. MD5 : 128bit 현재는 뚫려서 안 씀. 보안성이 민감하지 않은 정도에만 사용한다.
2. SHA -1 : 160 bit
3. SHA-2 : SHA-1에서 bit수만 늘렸다. 길이를 늘려 충돌성을 낮췄다.
4. SHA-3 : 앞선 2개와 완전히 다르다. keccak을 추가해 보안성이 높다. 보안이 각별히 필요한 경우에 사용한다.
해시함수 사용예시
1. Message Authentication Code (MAC)
해시 함수의 단방향성을 활용해 메시지의 무결성을 확인할때 사용한다.
보낸 메시지가 h(M)이라면 M을 해시함수에 넣어 실제 결과가 h(M)인지 확인하는 것이다.
.2. Online Bidding System.
BId할 금액의 해시값을 제출한다.
해시의 충돌성과 단방향성을 활용한 방식이다.
충돌성 : bid를 바꿀 수 없게한다. -> 충돌이 쉽게 일어나지 않으니 바꾸면 결과가 달라질 것이다. 따라서 못바꾸게 만든다!
단방향성 : 해시값을 보고 원래 입찰 금액을 알 수 없다. 따라서, 상대의 입찰금액을 알 수 없다.
3. Spam Reduction
공격자에게 메일을 보내기전, 추가적인 작업을 요구한다. (블록체인 채굴과 유사한듯)
보낼 메시지를 M, 현재 시간을 T, 송신자가 찾아야할 값 R을 놓는다.
송신자는 Hash를 통해 h(M,R,T)==S를 보내야하는데 수신자는 'S의 첫 N개의 bit가 0으로 시작해야한다'와 같은 제약 조건을 걸 수 있다. 따라서, 송신자는 메시지를 보낼때마다 해당 조건을 만족하는 R을 찾아야하고 이는 컴퓨팅 연산을 소모한다. 따라서 악의적인 스팸 메일을 보내는 자의 작업이 귀찮아 지는 것이다.
송신자는 해당 조건을 만족하기 위해 2^N의 해시연산을 해야한다.
그러나, 수신자는 결과 검증만 하면되기에 1번의 해시연산을 하면 된다.
송신자에게 부담이 가해진 것이다.
물론 N을 적절히 선정해 일반 사용자는 메일을 편하게 보내고, 악성 공격자(스팸메일발송자)는 메일을 보내는데 연산을 많이 소모하게 설정해야한다.
'CS > 정보보안' 카테고리의 다른 글
| 정보보안_6_Protocol (0) | 2023.04.22 |
|---|---|
| 정보보안_5_Authentication (0) | 2023.04.20 |
| 정보보안_4_Crypto (0) | 2023.04.14 |
| 정보보안_3_Crypto (0) | 2023.04.13 |
| 정보보안_1_introduction (0) | 2023.04.11 |
